主題四 解一元一次不等式 不等式x>-3,很容易看出它的解。 但不等式 3x2>11 你看得出來嗎? 可以慢慢代入檢驗啊! 別急!讓我來問你個問題。 阿兩帶了0 元逛夜市,花35 元買了一 杯珍珠奶茶。而後他看到了他最愛的射飛 鏢,一盤30 元。你認為阿兩最多歷史 古巴比倫留下的陶片顯示,在大約公元前00年(00 BC)古巴比倫的數學家就能解一元二次方程式了。在大約公元前480年,中國人已經使用配方法求得了二次方程式的正根。 公元前300年左右,歐幾里得提出了一種更抽象的幾何方法求解二次方程式。 7世紀印度的婆羅摩笈多(Brahmagupta)是第一※ 一元高次方程式: 解題步驟: (1) 用一次因式檢驗法,將原方程式做因式分解 (2) 各因式=0,求解未知數x ※ 分式方程式: 註:切記,x代回分母後,不能使分母為 0 (一) 一元一次方程式 1 試解下列各方程式: (1) 3(14 ) 50x =x,則x =_____。
初一应用题 一元一次方程应用题类型总结 习题二及答案15日更新 初中年级 家长帮
一元一次方程式公式
一元一次方程式公式-求一元一次方程式、二元一次聯立方程式、一元二次方程式、一元三次方程式的解。 解方程式 好用工具箱 Toggle navigation 好用工具箱十17 國中數學基本學習內容補救教材 第三冊 十17 主題四 解x 神奇法寶公式解 用公式法解一元二次方程式ax2 bx c = 0 的步驟如下: (一) 找出二次項係數a,一次項係數b,常數項c。 (二) 算出b2-4ac 的值。 (三) 若 b2-4ac > 0,則 x = − Õ±√ Õ 2−4 Ô Ö 2 Ô



一元二次方程的求根公式 星火网校
次方程式﹐但至少到西元100 年才發現了代數公式來表示其根﹒ 所謂方程式的代數公式解就是由方程式的係數經過四則運算與開方等有理運算所得的解﹐通常稱 為根式解(solution by radicals)﹒例如﹕ 一元一次方程式 b 0 的根式解為 b x a ﹒ 又一元二次方程式 c2 0 的一元二次方程式的根與係數的關係 在41 節的想想看中,我們請同學觀察兩根的和、兩根的積與原方程 式的係數之間的關係。現在,我們來對這些關係做說明。 設α、β為方程式ax bx c2 =0的兩個根,因此ax bx c2 =0可化 成ax x()( )−−=α β 0。我們知道認識完一元二次方程式後,接下來介紹一元二次方程式的解。 先回想一下,我們以前曾經在國七時學過一元一次方程式的解。 有一個一元一次方程式 −2=3 ,我們知道這個方程式中的 是 一個 未知數,而當我們將 =5 代入 −2=3 這個方程式時,會發現等式成
7a03 能理解一元一次方程式及其解的意義,並能由具體情境中列出 一元一次方程式。 七年級 7a04 能以等量公理解一元一次方程式,並做驗算。 七年級 7a05 能利用移項法則來解一元一次方程式,並做驗算。認識完一元二次方程式後,接下來介紹一元二次方程式的解。 先回想一下,我們以前曾經在國七時學過一元一次方程式的解。 有一個一元一次方程式 −2=3 ,我們知道這個方程式中的 是 一個 未知數,而當我們將 =5 代入 −2=3 這個方程式時,會發現等式成附註:關於一元三次多項方程式公式解的發現過程 1義大利數學家盧卡•帕西奧利於1494 年撰寫了一部名為《算術大全》的書,書中論述了一 次方程式和二次方程式的公式解,其中以符號代表未知量的手法,創造了原始的符號代數
附註:關於一元三次多項方程式公式解的發現過程 1義大利數學家盧卡•帕西奧利於1494 年撰寫了一部名為《算術大全》的書,書中論述了一 次方程式和二次方程式的公式解,其中以符號代表未知量的手法,創造了原始的符號代數求根公式 dao 为:x1=(b(b^24ac)^1/2)/2a ,x2=(b(b^24ac)^1/2)/2a 扩展资料 韦达定理说明了一元二次方程中根和系数之间的关系。 法国数学家弗朗索瓦·韦达于1615年在著作《论方程的识别与订正》中建立了方程根与系数的关系,提出了这条定理。33 一元一次方程式的列式與解法(1) 33 一元一次方程式的列式與解法(2) 33(1) 33(2) 選擇題:5 填充題:10 綜合題:4 a133(1) a133(2) 第三章 總複習(一) 第三章總複習(二) 選擇題:5 填充題:10 綜合題:4 選擇題:35題



數學7上 26道商品利潤問題 培優一元一次方程應用題 有答案 每日頭條


悟空问答 初一学生数学只考了1分 一元一次方程听不懂该怎么办 46个回答
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators一元一次方程式《各校考題─應用題03》 一元一次方程式《測驗01 ─ 解方程式》 一元一次方程式《測驗02 ─ 應用問題》 42 配方法與公式解求解《課程內容─12年版》 43 一元二次方程式《應用題》一元二次方程式的根與係數的關係 在41 節的想想看中,我們請同學觀察兩根的和、兩根的積與原方程 式的係數之間的關係。現在,我們來對這些關係做說明。 設α、β為方程式ax bx c2 =0的兩個根,因此ax bx c2 =0可化 成ax x()( )−−=α β 0。我們知道


悟空问答 如何解决一元一次方程的应用题 有哪些技巧 4个回答
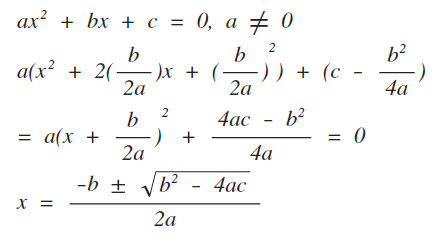


高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium
出版日期12年10月 名詞解釋 含有一個或一個以上的未知數並結合等號的數學式,稱為方程式。例如: 都是一元一次方程式, 是二元一次方程式, 是一元二次方程式。 備註一元二次方程式的公式解及二次函数图形 演讲稿 工作总结 调研报告 讲话稿 事迹材料 心得体会 策划方案 一元二次方程式的公式解及二次函数图形 个人整理的,觉得很好,就上传到文库与大家一起一元一次方程式《期末考》 42 配方法與公式解求解《課程內容─12年版》 43 一元二次方程式《應用題》 43 應用問題《考古題解》 4T 一元二次方程式《基測經典》 國一下數學實錄 nash;



解方程式公式图片 第1页 一起扣扣网



一元一次方程应用题公式汇总 知乎
一元一次方程式《期末考》 42 配方法與公式解求解《課程內容─12年版》 43 一元二次方程式《應用題》 43 應用問題《考古題解》 4T 一元二次方程式《基測經典》 國一下數學實錄 nash;42配方法與公式解 43解一元二次方程式 21直角座標平面 21生活中的平面圖形 21立體圖形 22二元一次方程式的圖形步驟2:將各數量的關係列成一元一次方程式。 步驟3:解一元一次方程式 步驟4:將方程式的解代回原問題中,檢驗後依題意寫答。 例1 倍數問題 這次段考,光耀的國文成績為x 分,如果光耀的數學成績是國文成績的2 倍少40 分,且這兩 科的成績合計為170 分。



一般 解一元一次方程式 等式兩邊未知數的比較 待下架影片 均一教育平台



用公式解解一元二次方程式 Youtube
342配方法與公式解doc 檢視 下載 122k 第 4 版 14年1月12日 下午853 陳端國 ĉ 343解一元二次方程式doc 檢視 下載 326k 第 5 版 14年1月15日 上午429 陳端國About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators3解一元一次方程式(含等量公理) 歡迎蒞臨教育部『 國民中學學習資源網 』網站,建議使用Internet Explorer50、Netscape60以上版本,瀏覽器及解析度1024*768


一元一次方程的计算和练习题 附答案 职场达人网 职场知识 职场礼仪 职场法则


回归直线法公式快速记忆法 一元一次方程 文库分享网
認識完一元二次方程式後,接下來介紹一元二次方程式的解。 先回想一下,我們以前曾經在國七時學過一元一次方程式的解。 有一個一元一次方程式 −2=3 ,我們知道這個方程式中的 是 一個 未知數,而當我們將 =5 代入 −2=3 這個方程式時,會發現等式成從文字翻譯到數學的應用關係 年級 國中 1, 教科書 南一 第一冊, 單元 31 以符號列式與運算, Keyword 數學,一元一次方程式一元二次方程式的公式解及二次函数图形 演讲稿 工作总结 调研报告 讲话稿 事迹材料 心得体会 策划方案 一元二次方程式的公式解及二次函数图形 个人整理的,觉得很好,就上传到文库与大家一起



一元一次方程应用题公式汇总 知乎


图解名校初中数学压轴题 代数第11章一元二次方程
3解一元一次方程式(含等量公理) 歡迎蒞臨教育部『 國民中學學習資源網 』網站,建議使用Internet Explorer50、Netscape60以上版本,瀏覽器及解析度1024*768一元一次方程式也被稱為線性 方程式,因為在笛卡兒坐標系上任何一個一次方程式的圖形都是一條直線。 組成一次方程式的每一項必須是常數或者是一個常數和一個變數的乘積。 且方程式中必須包含一個變數,因為如果沒有變數只有常數,式子則是代數式而非方程式。第三章一元一次方程式 一次式的運算一次式的運算 數字的抽象化數字的抽象化 在章節31中,我們學會了如何以符號代表數,而從32開始,我們才可以 把符號代表成一個任意數,而公式也只是把數字換成一個可以用任意數帶入的符


一元一次方程 一元一次方程 一元一次方程式 一元一次方程应用题 一元二次方程 一元一次方程练习题 一元一次方程的解法 一元一次方程ppt 一元一次 不等式 数学黑洞 一元二次方程求根公式 淘书楼图库



从一元一次方程到伽罗瓦理论 数学科普 伽罗瓦理论到底有多伟大 千年数学难题直接沦为简单推论 小馬锅的博客 Csdn博客
一 12 解二元一次聯立方程式 1 二元一次聯立方程式 2 代入消去法 3 加減消去法 主題1 二元一次聯立方程式 列二元一次聯立方程式 還記得第 6 頁的情境嗎?已知全票一張 x 元、半票一張 y 元, 小妍買 3 張全票和 1 張半票,共花了 700 元,可列出方程式:3x+y=700; 小翊買 5 張全票和 2 張半票,共花3 一元一次方程式 31 以符號列式與運算 311 一元一次式的意義、值與化簡 32 一元一次方程式的列式與求解 312 一元一次方程式的列式與解 313 解一元一次方程式 33 一元一次方程式的應用 314 一元一次方程式的應用問題3 一元一次方程式 31 以符號列式與運算 311 一元一次式的意義、值與化簡 32 一元一次方程式的列式與求解 312 一元一次方程式的列式與解 313 解一元一次方程式 33 一元一次方程式的應用 314 一元一次方程式的應用問題



七年级数学 如何用一元一次方程来解行程问题中的相遇问题 每日头条



初中数学方程公式图片 第1页 一起扣扣网


一元一次方程解决问题公式大全11 Doc 沃文网wodocx Com



初中数学方程公式图片 第1页 一起扣扣网


一元一次方程练卷 一元一次方程应用题 一元一次方程计算题 一元一次方程怎么解



初中数学 中考数学题型讲解代数式方程式求解



解一元一次方程式 移項法則 Youtube


二元一次方程的解法和公式有哪些 高三网



Matlab 解一元一次 一元二次 方程 史黑黑嘿嘿呦的博客 Csdn博客 Matlab解一元二次方程



二次方程 维基百科 自由的百科全书



一元一次方程 只含有一個未知數 即 元 並且未知數的最高次數為 華人百科



ひどい2 元1 次方程式 壁紙配布



一元一次方程 一元一次方程 一元一次方程式 一元一次方程应用题 一元二次方程 一元一次方程练习题 一元一次方程的解法 一元一次方程ppt 一元一次 不等式 数学黑洞 一元二次方程求根公式 淘书楼图库



國中數學公式解解一元二次方程式 Youtube



一元一次方程几年级学 一元一次方程是几年级学的 一元二次方程几年级 二元一次方程几年级


课程信息 本讲教育信息 一 教学内容 用配方法和公式法解一元二次方程 1 知道配方法的意义及用配方法解一元二次方程 的主要步骤 能够熟练地用配方法解系数较简单的一元二次方程 2 理解用配方法推导出一元二次方程的求根公式 了解求根公式中的


韦达定理 一元二次方程根与系数的关系 科普中国



翻轉學習影片 國中 數學 一元一次方程式 應用問題 練習6 速度公式


一元二次方程公式法 腾讯视频



一元次方程题图片 第1页 一起扣扣网


一元一次方程


一元二次方程公式法 腾讯视频


初一应用题 一元一次方程应用题类型总结 习题二及答案15日更新 初中年级 家长帮



求解一元三次方程



方程虚根的求根公式


一元一次 初中数学一元一次方程知识点总结



一元一次方程打折问题 每日头条



01一元一次方程的概念一元一次方程初中数学初一 Youtube


解二元一次方程的公式 解一元二次方程的公式 二元一次方程的公式 二元一次方程求解公式


小学解方程公式 小学四年级数学学的公式 尚书坊



例題 克拉瑪公式解二元一次方程組 Youtube


三元一次方程式求連比 紀算 補習班 數學補習班 三重 文理補習班 數學公式 數學題庫 數學競賽 國小數學 國中數學 痞客邦


中考数学 考前总复习 公式定义总结 二 一次方程


韦达定理 一元二次方程根与系数的关系 科普中国



微博搜索



七年级数学一元一次方程知识点归纳 知乎


一元一次方程解决问题公式大全11 Doc 沃文网wodocx Com
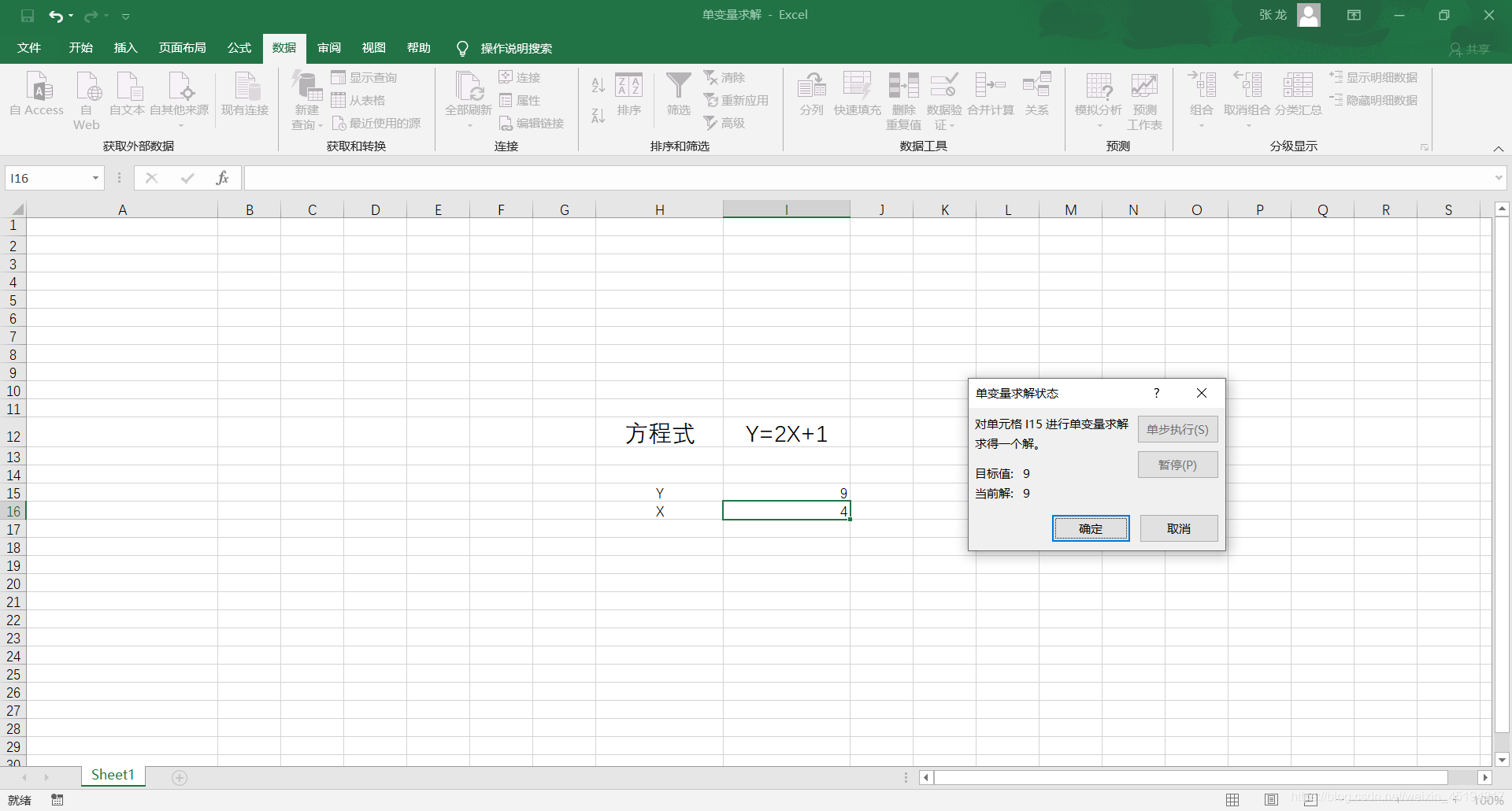


如何使用excel对一元一次或多次方程求解 单变量求解工具的使用 Weixin 的博客 Csdn博客



七年级数学一元一次方程知识点归纳 知乎



Excel解一元三次方程 Excel一元一次方程 Excel解三元一次方程组 Excel如何解方程


從推導一元二次方程的公式解看個性 線代啟示錄



一元二次方程的求根公式 星火网校



初二数学应用题训练3下载 Word模板 爱问共享资料



一元一次方程双十一性价比高品牌选购推荐 淘宝海外



4 2配方法與一元一次方程式的公式解 學生練習11 Youtube


一元二次方程公式法 腾讯视频



例題 一元二次方程式公式解 方程式的解有根號 配方法與公式解 均一教育平台



二元一次方程的公式是什么 高中知识网



七年級數學 12道經典一元一次方程解行程問題專項大演練 每日頭條


一元一次方程认识及基本解法 松鼠文库



一般 解一元一次方程式 分數型 Youtube


二元一次方程两根之和两根之积公式 初三网



翻轉學習影片 國中 數學 一元一次方程式 應用問題 練習2



一般 解一元一次方程式 分數型判斷相同的解 待下架影片 均一教育平台



陳力數學7上解一元一次方程式1 Youtube


一元一次方程解决问题公式大全11 Doc 沃文网wodocx Com


初中数学重要公式定律 一元一次方程 一元一次方程资讯 新东方在线移动版



一元二次方程求根公式 小知识网


一元二次方程公式法 腾讯视频



卡尔丹公式推导全过程 一元三次方程卡尔丹公式例题图解 景清网



一元二次方程知识点解析和题型汇总 知乎



國中數學的 數學b1全 整數 分數 一元一次方程式筆記 Clear


初一数学周末培优训练十 一元一次方程二以及简单应用题 下载 Word模板 爱问共享资料


答疑系列 初一数学 含参一元一次方程 绝对值方程的求解 例5 哔哩哔哩 つロ干杯 Bilibili



七年级数学下册课后补习班辅导一元一次方程2讲学案苏科版下载 Word模板 爱问共享资料



Qflqassithi76m



一次方程式計算 Hd壁紙画像fhd



翻轉學習影片 國中 數學 一元一次方程式 應用問題 練習1



一元二次方程的解法公式有哪些 一元二次方程的图像 星火网校



初中数学一元一次方程定义和相关知识点 星火网校



一元一次方程应用题公式汇总 知乎



Python教程7 Python解二元一次方程ax Bx C 0 It云清 Csdn博客



一元一次方程应用题公式汇总 知乎


測評網 國一下 數學第一次段考 複習錦囊



初中数学重点突破 一元一次方程相关的6类问题 含例题和解析 每日头条



解一元二次方程题图片 第1页 一起扣扣网


分母是小数的一元一次方程的解法秘籍 哔哩哔哩 つロ干杯 Bilibili


克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌


气态方程公式讲解 腾讯视频


解二元一次方程的公式 解一元二次方程的公式 二元一次方程的公式 二元一次方程求解公式



九级数上册二一元二次方程用公式法求解一元一次方程作业设计 新版 北师大版下载 Word模板 爱问共享资料


一元二次方程公式法 腾讯视频



二次方程 维基百科 自由的百科全书



一元一次方程式應用題 3 速度公式 Youtube



0 件のコメント:
コメントを投稿